(Pro)seminar on computer-assisted mathematics

Organisation

The purpose of this (pro)seminar is give an introduction to computer-assisted mathematics, in particular the computer algebra system Sage and the interactive theorem prover Lean.

• Target audience: Bachelor students.
• Language of instruction: English.
• Time and place: 4-6pm on Wednesdays, in Seminar Room Statistik (INF 205).
• Zulip channel:     (please contact me by email to register).
• GitHub repository:   Comp_assisted_math (branch: 2023_SoSe)  
• Online classroom: Zoom coordinates sent through Müsli and available on the Zulip channel.

This seminar is intended for beginners. More experienced students are welcome to participate as mentors/tutors.

Program

Topics of linear algebra to be covered in the seminar:

• Computer algebra systems. Representations of vectors and matrices.
• Row operations. Gaussian elimination. Row-reduced echelon form of a matrix.
• Invertible matrices. Elementary matrices. Determinant.
• Linear independence. Bases for the kernel and the image of a linear transformation.
• Rank-nullity theorem and the row space of matrix. Basis for the row space.
• Base change. Coordinates of a vector, matrix of a linear transformation.
• Eigenvalues and the characteristic polynomial. Diagonalisation.
• The Gram-Schmidt process. Least-square approximation.

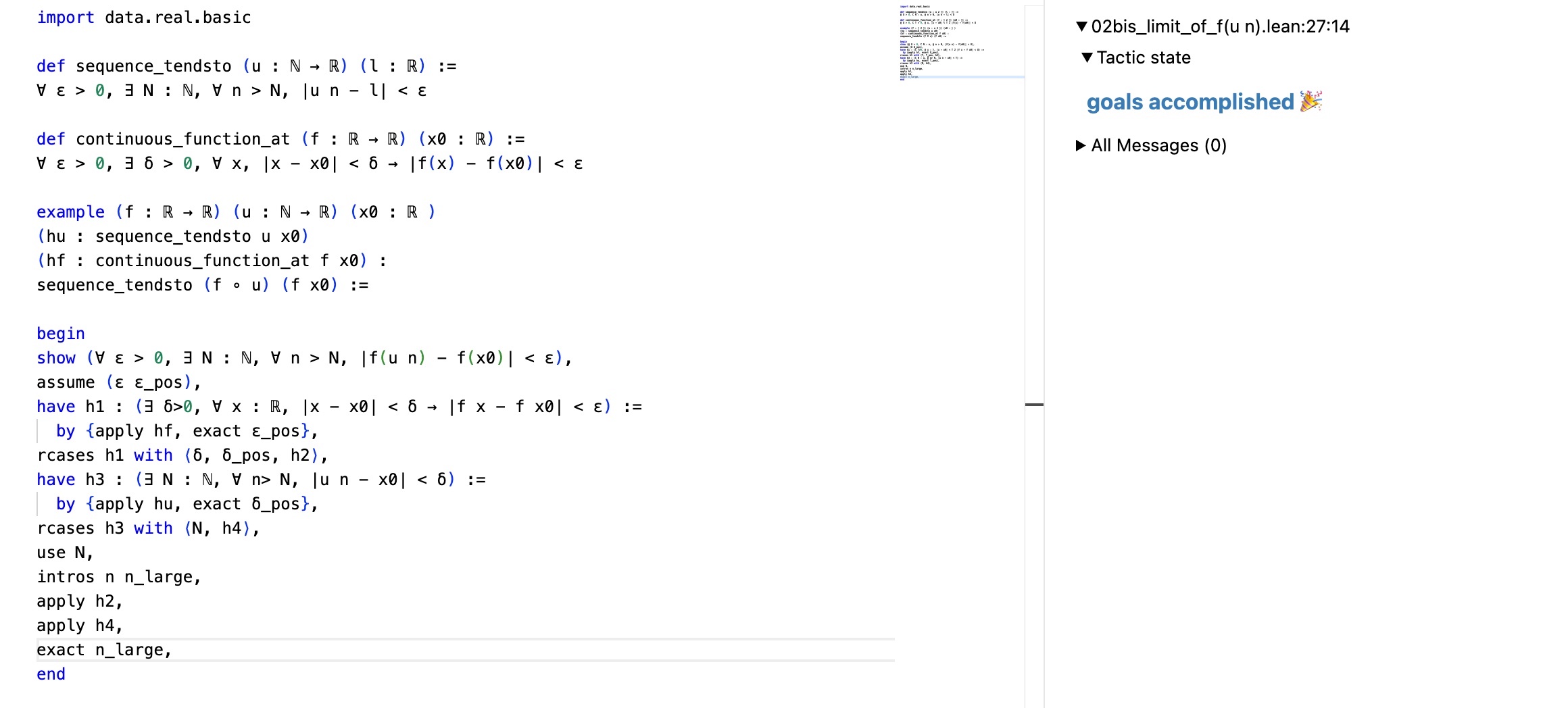
Aspects of the Lean programming language to be covered in the seminar:

• Installation of a proof assistant. Familiarisation with the interface.
• The Natural Number Game (Peano axioms and the induction principle).
• Equality and computations (tactics to prove algebraic identities).
• Implications and equivalences (propositional logic).
• Predicates and quantifiers (first-order logic).
• Contraposition and proof by contradiction (proof tactics).
• Formalisation of basic mathematical statements.