Matemáticas, lógica e informática

60 años de la carrera de matemáticas
Celebración en honor a Xavier Caicedo
Universidad de Los Andes, Diciembre 2024

Florent Schaffhauser
Universidad de Heidelberg

Cronograma

• Clase 1: Introducción a Lean.
• Clase 2: Tácticas básicas.
• Clase 3: Tipos dependientes.
• Clase 4: Estructuras algebraicas.

Organización del curso

• En cada sesión: Clase + Ejercios prácticos (archivos proporcionados).
• Se recomienda trabajar en parejas.
• No hay necesidad de instalar Lean (pero es buena idea hacerlo).

¡Únase al siguiente canal de Zulip para tener acceso a los archivos del curso y hacer preguntas sobre los temas vistos en clase!

Zulip channel

Clase 1 - Introducción a Lean

1. ¿Cómo utilizar Lean?
2. El ecosistema de Lean
3. Sintaxis básica

¿Cómo utilizar Lean?

• En un navegador web.
• En un IDE (Integrated Development Environment).
• En un app.

¿Qué es Lean?

• Lean es un lenguaje de programación creado por Leonardo De Moura, de Microsoft Research, en el 2013. La versión actual es Lean 4. No es compatible con Lean 3.
• Es un lenguaje declarativo, estáticamente tipado, y con capacidades de inferencia de tipos (como Haskell).
• Lean maneja funciones dependientemente tipadas, lo cual es de gran utilidad en su uso como asistente de prueba.
• Es un lenguaje de programación funcional, y como tal se caracteriza por la inmutabilidad de estados y la ausencia de efectos secundarios.

Declarar una función

El siguiente código declara en Lean la función que envía el número natural a .

def square : Nat → Nat := fun (n : Nat) ↦ n * n

• def es una palabra clave del lenguaje: se usa para declarar una función. El término square es el identificador que hemos escogido para la función.
• Nat → Nat es la signatura (o el tipo) de la función square.
• fun (n : Nat) ↦ n * n es la definición como tal de la función square (esa definición aparece después del :=).

El verificador de tipos acepta esa declaración porque n * n es un término de tipo Nat, por definición de la operación *. La versión anotada de la expresión n * n sería (Nat.mul : Nat → Nat → Nat) (n : Nat) (n : Nat). Eso lo infiere el verificador.

Usar Lean en línea

• Se puede usar Lean a través de la página Lean 4 Web server.
• Aquí está un archivo de introducción a la sintaxis de Lean:
  Basic Lean syntax
• El servidor es útil para cargar un solo archivo y trabajar en ello (no sirve para proyectos con más de un módulo). También se puede bajar el archivo modificado después de trabajar en ello. Y el servidor les da acceso a la librería Mathlib (la principal librería matemática de Lean).

Usar Lean en un IDE

• También se puede instalar Lean localmente y trabajar en un editor de texto.
• Uno de los más populares entre los utilizadores de Lean es VS Code con la extensión Lean 4:
  

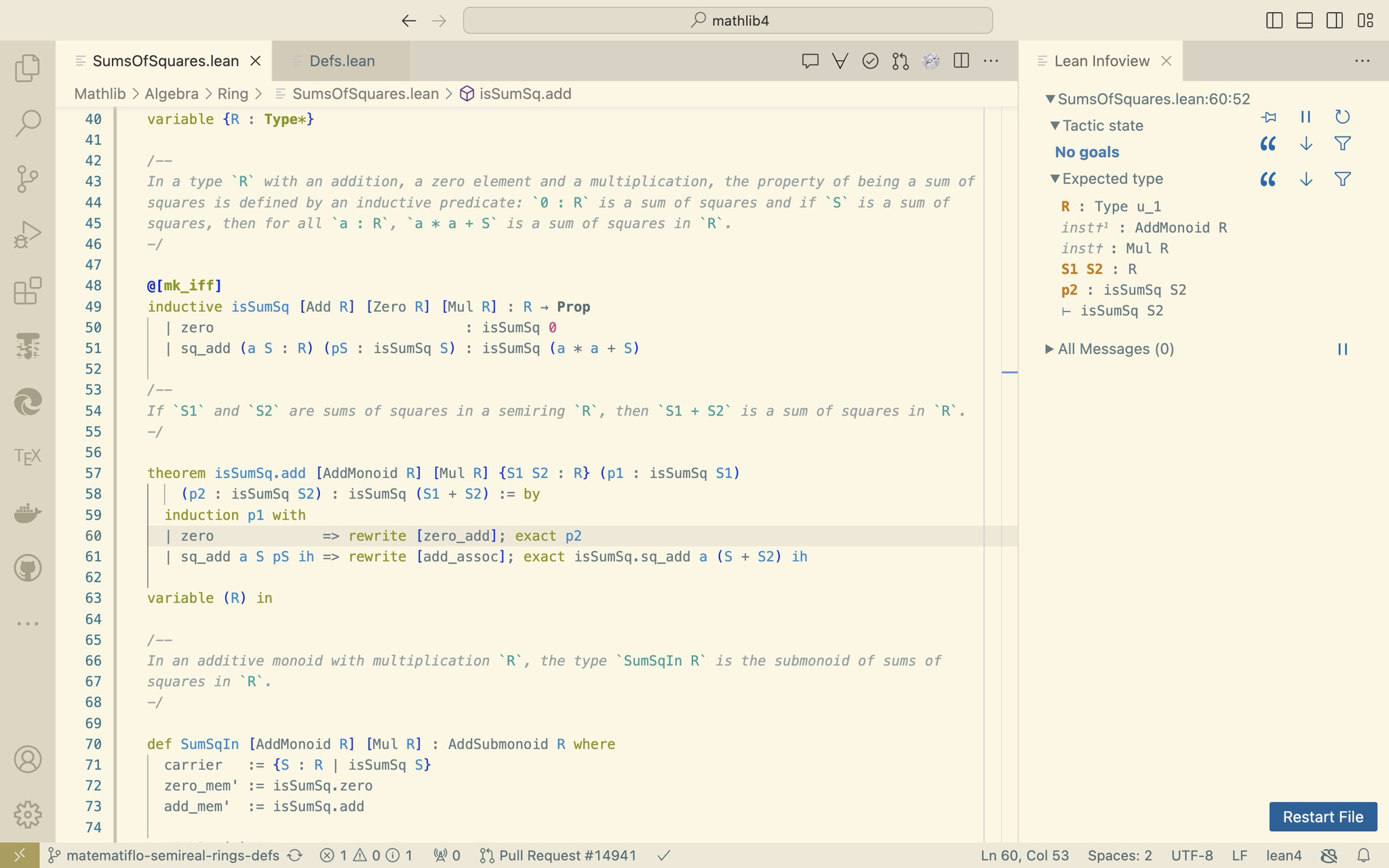
Instalación de Lean

• Es posible instalar Lean directamente desde VS Code, utilizando la extensión Lean 4 (requiere instalar git primero).
• Para una instalación más controlada, instalen primero elan (el version manager de Lean), luego instalen Lean con el comando elan install stable. Para iniciar un proyecto nuevo, sigan las instrucciones del manual oficial de Lean.
• Todo lo anterior se puede encontrar, con instrucciones más detalladas, en la página de la Leanprover Community:
  

Recursos en línea para empezar

• La página oficial de Lean.
• La página de la comunidad de Lean website.
• Un canal de Zulip dedicado a Lean.

El servidor de juegos

• Existe un servidor de juegos de Lean, albergado por la Universidad Heinrich Heine, en Düsseldorf.
• El primer juego fue el Natural Number Game, creado por Kevin Buzzard, Mohammad Pedramfar (para la versión original, en Lean 3) y Jon Eugster.
• Este juego proporciona una introducción al lenguaje Lean 4, a través de una demostración de las principales propiedades de los enteros naturales. ¡Les recomiendo que lo prueben hoy mismo!
  

El ecosistema de Lean

• Bibliotecas.
• Proyectos colaborativos.
• Documentación, motores de búsqueda, y hasta más.

Bibliotecas de Lean

Lean viene con una biblioteca básica incluída. El módulo Init.Prelude es importado automáticamente cuando se crea un archivo Lean nuevo.

Hay otras bibliotecas, que pueden ser utilizadas como dependencies en un proyecto Lean dado:

• Mathlib: una biblioteca matemática mantenida por sus utilizadores (nivel investigación).
• Batteries: una extensión de la biblioteca básica, destinada para ser usada en matemáticas y en informática.
• SciLean: una biblioteca de cálculo científico en Lean.

Tanto Lean como sus bibliotecas son de código abierto (bajo una licencia Apache 2.0).
El código está de libre acceso en GitHub.

Mathlib

• Mathlib es un esfuerzo comunitario para construir una biblioteca unificada de matemáticas formalizadas en el asistente de prueba Lean.
• A octubre de 2024 cuenta con más de 350 colaboradores y 1.5 millones de líneas de código.
• Mathlib ya contiene muchas matemáticas de nivel universitario y de investigación. Es un proyecto académico al que cualquiera puede contribuir.
• Ya se está utilizando en varios proyectos colaborativos en línea. Algunos de ellos involucran a medallistas Fields como Peter Scholze y Terence Tao.

Proyectos Colaborativos en Línea

• El objetivo de un proyecto de este tipo es formalizar un pedazo de matemáticas. Esto significa al menos dos cosas:
  1. Encontrar una manera de representar objetos matemáticos en un lenguaje de programación.
  2. Usar las reglas de tipaje de ese lenguaje de programación para verificar si una declaración matemática es sintácticamente correcta.
• Varios proyectos de formalización en Lean están enfocados a la verificación de pruebas matemáticas, en una variedad de áreas de investigación:
  • El Liquid Tensor Experiment (matemáticas condensadas).
  • El Teorema de los Números Primos.
  • El teorema de la inversión de la esfera.
  • El teorema de Carleson generalizado.

Herramientas de colaboración

• Un proyecto de formalización puede involucrar a decenas de personas diferentes. Al dividir el proyecto en objetivos, se vuelve posible la participación de personas procedentes de áreas de investigación distintas o que estén en diferentes etapas de su carrera profesional.
• La discusión ocurre en línea, en el canal de Lean en Zulip, y el repositorio de código se aloja en GitHub o en un servicio similar.
• Algunos esfuerzos recientes incluyen el desarrollo de la automatización de ciertas tareas, a veces utilizando modelos de lenguaje grandes (IA).

Blueprints

• Un Lean blueprint establece una interfaz entre un texto matemático en el sentido clásico, escrito en , y su contraparte en código Lean.
• Genera un gráfico de dependencias, mostrando el avance del proceso de formalización (enuncidao sin formalizar, enunciado formalizado, prueba formalizada).
• El blueprint se actualiza a medida que se escribe el código Lean.

El blueprint del teorema de Fermat

Kevin Buzzard está liderando actualmente la formalización del Último Teorema de Fermat (2024-2029). El plan de la prueba se puede visualizar de la siguiente manera gracias a Lean blueprint:

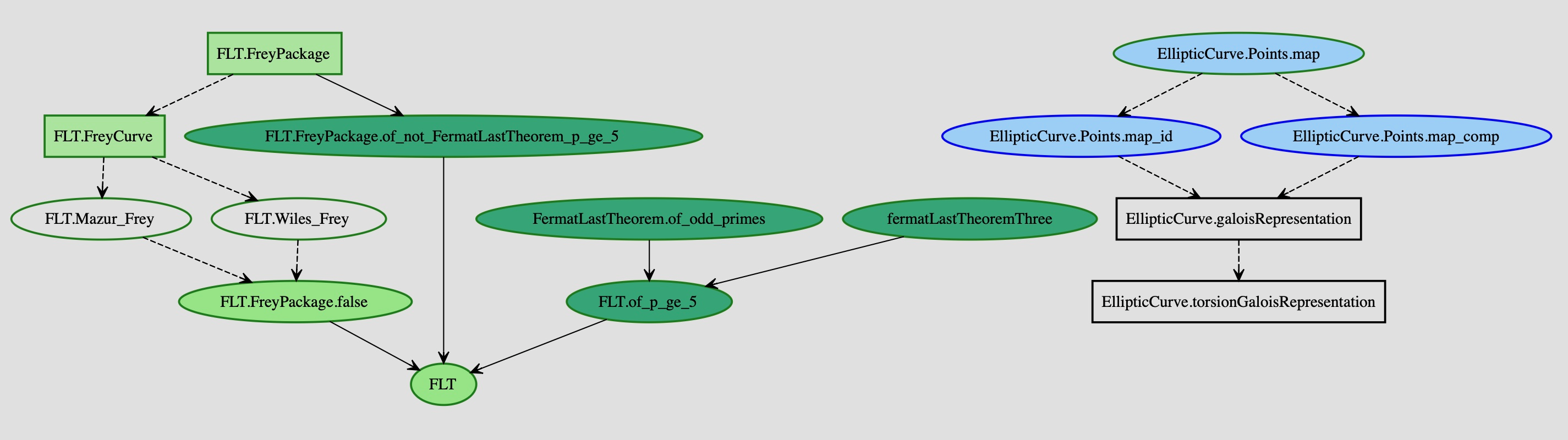
El código de colores muestra el avance del proyecto hacia su finalización.

Documentación

Las siguientes herramientas son indispensables para escribir código en Lean:

• La documentación de Mathlib. También incluye la biblioteca básica de Lean y Batteries. La búsqueda se realiza por nombre (identificador).
• Loogle: el motor de búsqueda oficial del lenguaje Lean. Es posible buscar por una signatura de tipo dada, como (?a -> ?b) -> List ?a -> List ?b.
• Moogle y LeanSearch: motores de búsqueda impulsados por IA. Allí se puede usar lenguaje natural, como ​order subgroup divides order group o dim V = dim (Ker u) + dim (Im u).

Manuales de referencia

Los siguientes libros en línea son las referencias estándar de la comunidad Leanprover:

• Theorem Proving in Lean 4, por Jeremy Avigad, Leonardo de Moura, Soonho Kong y Sebastian Ullrich (basado en la versión de Lean 3 de 2017).
• Mathematics in Lean, por Jeremy Avigad y Patrick Massot (2020).
• Mechanics of Proof, por Heather MacBeth (2022-2024).
• Functional Programming in Lean, por David Thrane Christensen (2023).

Lake y Reservoir

• El package manager de Lean se llama Lake (lean make). Se utiliza para compilar programas en Lean.
• Para iniciar un proyecto en Lean, se puede usar lake init o lake new (prueben lake --help primero). Esto también se puede hacer directamente desde VS Code, usando la extensión de Lean 4.
• Los paquetes de Lean pueden alojarse en Reservoir, el registro de paquetes de Lean.

Sintaxis básica en Lean

1. Términos y tipos
2. Funciones currificadas
3. Tipos inductivos

¿Qué es un tipo?

Dependiendo de a quién le pregunten, un tipo puede ser visto como:

• Una anotación a un término, controlando las operaciones permitidas sobre ese término: (3 : Nat), (-4 : ℤ), ([1, 2, 3] : List Nat), (Nat.mul : Nat → Nat → Nat).
• Una lista de reglas para introducir y eliminar ciertos términos.
• Un buen sustituto para la noción de espacio topológico.

Cada término tiene un tipo asignado, que es parte de su definición como término: dado que no tienen el mismo tipo, (3 : Nat) y (3 : ℤ) son objetos diferentes. Expresiones como x := x + 1 no están bien tipadas y no tienen sentido en un lenguaje de programación funcional.

Expresiones bien tipadas

En Lean, se puede averiguar el tipo de un término usando el comando #check:

#check 42             -- 42 : Nat
#check Nat            -- Nat : Type
#check Nat.mul        -- Nat.mul : Nat → Nat → Nat
#check "42"           -- "42" : String
#check 1 + 1          -- 1 + 1 : Nat
#check 1 + 1 = 2      -- 1 + 1 = 2 : Prop
#check 1 + 1 > 2      -- 1 + 1 > 2 : Prop

Nótese que una expresión bien tipada puede ser reconocida como una proposición independientemente de si es "matemáticamente correcta". La expresión 2 + 2 = 5, por ejemplo, es sintácticamente correcta (una igualdad entre dos números naturales). En contraste, una expresión común como 2 * (3 + 1) = 2 * 3 + 2 * 1 = 8 no está bien tipada.

¿Para qué preocuparse?

Es de sentido común no mezclar cantidades que no están relacionadas entre sí. Aquí va un ejemplo de una suma mal tipada.

Image credits: MikeGogulski, CC BY-SA 3.0.

El desarrollo de la teoría de tipos

• Los tipos fueron introducidos por Bertrand Russell en 1912, con la esperanza de evitar la aparición de paradojas en la teoría de conjuntos.
• Su uso fue sistematizado y simplificado por Alonzo Church, quien introdujo el -cálculo (simplemente tipado) en 1940.
• En 1972, Per Martin-Löf desarrolló una teoría de tipos dependientes, la cual puede ser utilizada para proporcionar fundamentos alternativos para las matemáticas. Ésta es la lógica subyacente de Lean.
• En 1989, Thierry Coquand publicó la primera versión oficial de Coq (también conocido como Rocq), un asistente de prueba que soporta todos las estructuras linguísticas de la teoría de tipos de Martin-Löf.
• En 2013, Vladimir Voevodsky y sus colaboradores publicaron un tratado de Teoría homotópica de tipos y los fundamentos univalentes de las matemáticas.

Estructura de un asistente de pruebas

La arquitectura de un asistente de prueba interactivo se puede representar de la siguiente manera.

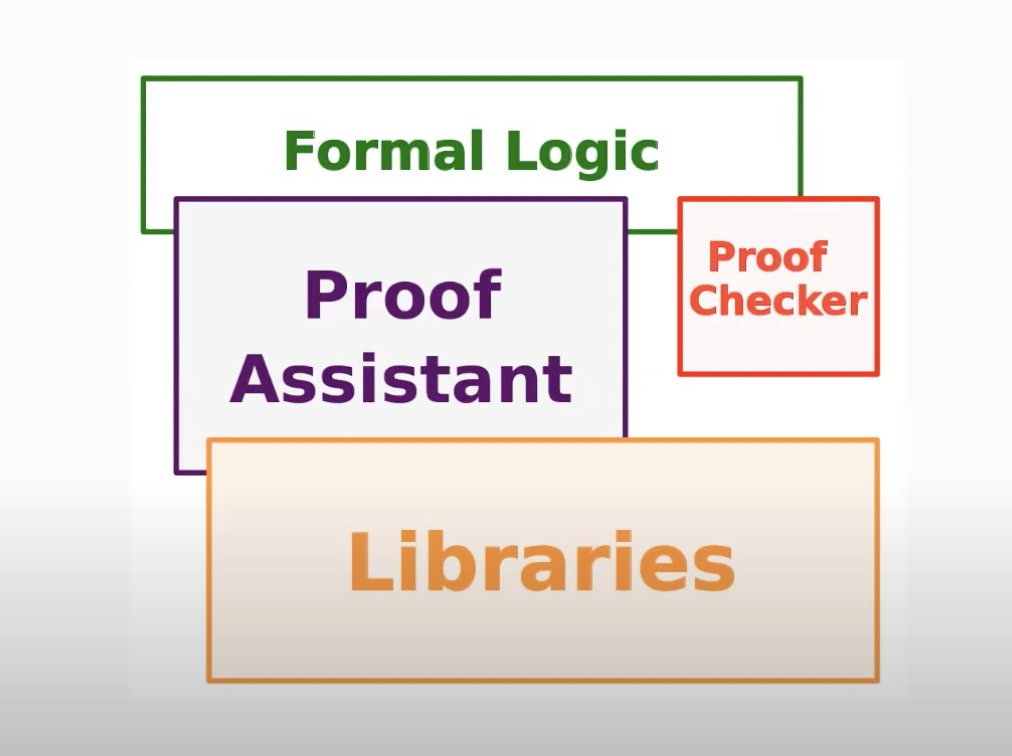Créditos de la imagen: Assia Mahboubi.

• Los usuarios humanos interactúan con el asistente de prueba escribiendo bibliotecas.
• El compilador verifica que el código sea sintácticamente correcto.
• La elección de la teoría de tipos como lógica subyacente es una decisión de diseño.

Funciones matemáticas

• Las funciones simplemente tipadas f : X → Y son los objetos básicos de un lenguaje como Lean.
• Su implementación puede verse similar a la definición matemática usual:

def fact : Nat → Nat
  | 0     =>  1 
  | k + 1 => (k + 1) * fact k

#check fact    -- fact : Nat → Nat

#check fact 5  -- fact 5 : Nat

#eval  fact 5  -- 120

Funciones currificadas

• En Lean, la forma natural de definir una función de dos variables es con notación currificada. En efecto, una función de dos variables puede ser reemplazada por una función que envía a una función de , es decir, .
• En un lenguaje de programación funcional, si escribimos f : A → B → C, entonces en la expresión f a b, el término f a es una función de B a C, y se aplica a b.

def sum : Nat → Nat → Nat := fun x y ↦ x + y

#check sum 3    -- sum 3 : Nat → Nat
#eval  sum 3 5  -- 8

Si en lugar de eso definimos def sum₁ : Nat → Nat → Nat := fun x ↦ (fun y ↦ x + y), entonces obtenemos sum = sum₁, por reflexividad.

Funciones de orden superior

• Podemos escribir funciones currificadas con un número arbitrario de variables: si f : A → B → C → D → E, entonces para todos a : A, b : B, c : C, d : D, tenemos f a b c d : E.
• Esto no es lo mismo que f : A → (B → C) → D → E, que toma como argumentos un término a : A, una función u : B → C y un término d : D, devolviendo un término de tipo E.

def f : Nat → (Nat → ℝ) → ℝ → ℝ := 
  fun (n : Nat) (u : Nat → ℝ) (x : ℝ) ↦ 2 ^ n * u n + x

def v : Nat → ℝ := fun n ↦ 2 * n

#eval f 3 v (-6)  -- 42

Tipos inductivos

El tipo inductivo más famoso en matemáticas es probablemente el tipo Nat, cuya definición se remonta a Giuseppe Peano en 1889.

inductive Nat : Type
  | zero : Nat
  | succ : Nat → Nat

Las definiciones inductivas producen funciones especiales llamadas constructores. En este caso, hay dos de ellos (dos reglas de introducción para términos de tipo Nat):

• Nat.zero : Nat (una función cuyo valor es su propio nombre se llama un átomo, pueden verla como una función del tipo Unit al tipo Nat, si prefieren).
• Nat.succ : Nat → Nat (la función sucesor), que dice que para cada n : Nat hay un término n.succ : Nat (dot notation para Nat.succ (n : Nat)).

El producto de dos tipos es un tipo inductivo

La definición del producto de dos tipos como un tipo inductivo es menos usual en matemáticas.

inductive Prod (X Y : Type) : Type
  | mk : X → Y → Prod X Y

Esto significa que los términos del tipo Prod X Y se introducen a través del constructor Prod.mk : X → Y → Prod X Y. En otras palabras, para todo x : X y todo y : Y, el término Prod.mk x y es de tipo Prod X Y y esta es la única regla de introducción que hay para términos de tipo X × Y. En Lean, el tipo Prod X Y se denota por X × Y y sus términos por ⟨x, y⟩ (corchetes angulares).

Funciones definidas en tipos inductivos

• Ya hemos visto ejemplos de funciones f : Nat → Nat, como la función factorial. Fue definida por inducción. Dado que el constructor Nat.succ es una función de Nat a Nat, el principio de inducción para Nat incluye una llamada recursiva: para definir f (n + 1), podemos usar n y f n, como en la definición de fact (n + 1).
• Sin embargo, la inducción no se limita a Nat: cada tipo inductivo tiene un principio de inducción asociado. Para el producto, implica en particular que, para definir una función f : X × Y → Z, basta con definirla en los términos canónicos Prod.mk x y. En la práctica, esto se hace a través de pattern matching (búsqueda de patrones).

def pr₁ {X Y : Type} : X × Y → X
  | Prod.mk x y => x

La suma de dos tipos

• La suma de dos tipos y también se define inductivamente.
• El tipo inductivo tiene dos constructores porque hay dos maneras de introducir términos de tipo : pueden provenir ya sea de o de $Y`.
• Para eliminar términos de tipo en , debemos especificar la definición de nuestra función en cada constructor. De nuevo, esto se hace a través de una búsqueda de patrones (análisis de casos).

inductive Sum (X Y : Type) : Type
  | inl : X → Sum X Y
  | inr : Y → Sum X Y

def charac_second_summand {X Y : Type} : X ⊕ Y → Bool
  | Sum.inl x => (false : Bool)
  | Sum.inr y => (true  : Bool)

Resumen y siguientes pasos

• Los lenguajes de programación funcional basados en la teoría de tipos dependientes con tipos inductivos (como Lean 4) pueden usarse para formalizar matemáticas.
• Verificación de tipos (type-checking) significa comprobar que nuestro código es sintácticamente correcto.
• Funciones currificadas y tipos inductivos se usan en una variedad de contextos y para muchos propósitos, en particular para formalizar matemáticas.
• A cada tipo inductivo se le asocia un principio de inducción. Esto nos permite definir funciones que salen de un tipo inductivo mediante búsqueda de patrones.
• ¡Ahora sí vamos a escribir código en Lean!

Archivo para practicar sintaxis de Lean y enlace al Natural Number Game

Sintaxis de Lean Natural Number Game

Dato curioso: visto a menudo en ejemplos de Lean, es el primo irregular más pequeño. Un número primo impar es irregular si existe un número natural tal que divide el numerador del -ésimo número de Bernoulli (criterio de Kummer).