Matematiflo

Organisation

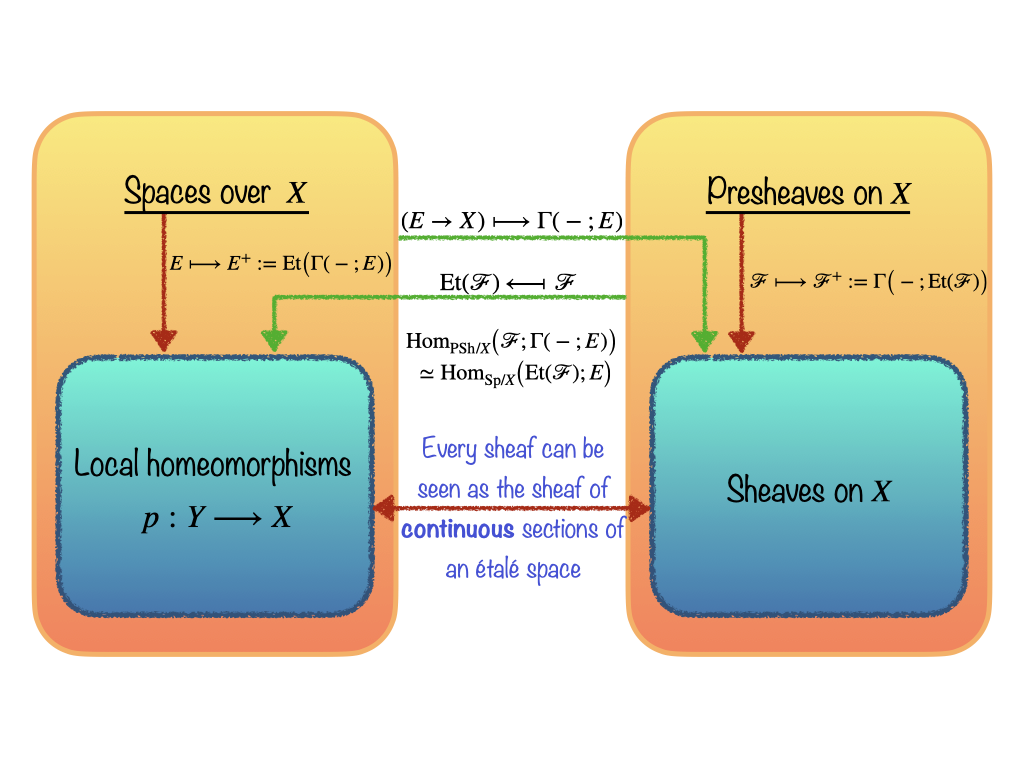
The purpose of this seminar is to cover the basics of sheaf theory, with a view towards the cohomology of real and complex manifolds. The expositions will be given by the participants, in coordination with the professor in charge of running the seminar.

Target audience: Master students and advanced Bachelor students.
Language of instruction: English.
Time and place: 4-6pm on Wednesdays, in Seminar Room 8 (INF 205).

This seminar can be recommended as a complement to the course on Real Algebraic Varieties, taught in Heidelberg during the Winter Semester 2022-2023.

The equivalence between sheaves and étalé spaces

References

B.R. Tennison, Sheaf Theory, Cambridge University Press (1975).
C. Voisin, Hodge Theory and Complex Algebraic Geometry: Volume I, Cambridge University Press (2002).

Schedule

#	Date	Topic	Speaker	References	Notes
1	05/10	Introductory meeting	Florent Schaffhauser		Syllabus
2	19/10	Presheaves and sheaves	Anna Roth	[Tennison] § 1, 2.1, 2.2
3	26/10	The sheafification of a presheaf	Immanuel Klevesath	[Tennison] § 2.3, 2.4
4	02/11	Covering spaces and locally constant sheaves	Florent Schaffhauser
5	09/11	Morphisms of presheaves and sheaves	Felix Preu	[Tennison] § 3.2-3.4, 3.6
6	16/11	Ringed spaces and manifolds	Till Janke	[Tennison] § 4.1, 4.3
7	23/11	Locally free sheaves and invertible sheaves	Elia Fiammengo	[Tennison] § 4.4, 4.5
8	30/11	An introduction to the Riemann-Hilbert correspondence	Florent Schaffhauser
9	07/12	Derived functors	Tim Wagemann	[Tennison] § 5.1, 5.2
10	14/12	Sheaf cohomology	Mario Bühler	[Tennison] § 5.3
11	11/01	Čech cohomology and the Picard group	Aarya Shah	[Tennison] § 5.4
12	18/01	Flabby, soft and fine sheaves	Theresa Häberle	[Voisin] § I.4
13	25/01	Cohomology of manifolds	Matilde Sciortino	[Voisin] § I.4
14	01/02	The Hodge decomposition theorem	Florent Schaffhauser	[Voisin] § II.5, II.6