Interactive Theorem Proving in Lean

Compact course
Heidelberg Graduate School
Mathematical and Computational Methods for the Sciences

Florent Schaffhauser
Heidelberg University

Outline of the lectures

• Lecture 1: An introduction to Lean
• Lecture 2: Basic tactics
• Lecture 3: Dependent types
• Lecture 4: Algebraic structures

Organisation of the workshop

• Each session: Lecture + Exercises. Practice files are provided.
• You are encouraged to work in pairs.
• No prior installation of Lean is required.

Join this Zulip channel and ask your questions there!

Zulip channel

Lecture 1 - An introduction to Lean

1. Using Lean
2. Lean's ecosystem
3. Basic Lean syntax

Using Lean

• In a browser
• In an IDE
• In an app

What is Lean?

• Lean is a programming language created by Leonardo De Moura at Microsoft Research in 2013. The current version is Lean 4. It is not backwards-compatible with Lean 3.
• It is a declarative, statically-typed programming language with type inference capabilities, like Haskell.
• Lean supports dependently-typed functions and inductive types, making it possible to use it as a theorem prover.
• It is a functional programming language, characterised by the immutability of states and the absence of side effects.

Declaring a function

The following is Lean code for the function sending a natural number to .

def square : Nat → Nat := fun (n : Nat) ↦ n * n

• def is the keyword to declare a function, square is our identifier for this function.
• Nat → Nat is the type signature of the function square.
• fun (n : Nat) ↦ n * n is the actual definition of square (appearing after :=).

This is accepted by the type-checker because n * n is a term of type Nat, where * has been previously defined. The type-annotated form of the expression n * n is (Nat.mul : Nat → Nat → Nat) (n : Nat) (n : Nat), which is inferred by the type-checker.

Using Lean online

• You can use Lean via the Lean 4 Web server.
• Here is a practice file on basic Lean syntax:
  Basic Lean syntax
• The server enables you to load and save single Lean files (not suitable for multiple files projects). It provides access to Mathlib (Lean's main mathematical library).

Using Lean in an IDE

• Alternatively, one can install Lean locally and open Lean files in a code editor.
• VS Code and the Lean 4 extension are a popular choice among Lean users:
  

Installing Lean

• It is possible to install Lean directly from within VS Code, using the Lean 4 extension (install git first if you do not have it on your machine).
• For a more controlled installation, first install elan (the Lean version manager), then install Lean by running elan install stable. To start a project, follow the instructions of the official Lean manual.
• You can find all of this and more detailed installation instructions on the webpage of the Leanprover Community:
  

Online resources to get started

• The official Lean webpage.
• The Leanprover community website.
• The Lean Zulip channel.

The Lean game server

• The Lean game server is hosted at the Heinrich Heine Universität in Düsseldorf.
• The first Lean game was the Natural Number Game, created by Kevin Buzzard, Mohammad Pedramfar (original Lean 3 version) and Jon Eugster.
• It provides an introduction to the Lean language via a construction of the main properties of the natural numbers. I encourage you to play it today!
  

Lean's ecosystem

• Libraries
• Collaborative projects
• Documentation, search engines and more

Available Lean libraries

There is a core library shipped with Lean. The file Init.Prelude is imported by default when you open a Lean file.

Other libraries can be used as dependencies in a Lean package:

• Mathlib: a user-maintained mathematical library (research-level).
• Batteries: an extended core library, for use in both computer science and mathematics.
• SciLean: scientific computing in Lean 4.

Lean and all the libraries above are open-source (under an Apache 2.0 license).
The code is freely accessible on GitHub.

Mathlib

• Mathlib is a community-driven effort to build a unified library of mathematics formalized in the Lean proof assistant
• As of October 2024: ~350 contributors, 1.5 million lines of code.
• Mathlib already contains a lot of university and research-level mathematics. It is an academic project, to which anyone can submit a contribution.
• It is already being used in major online collaborative research projects, some of them involving Fields medallists Peter Scholze and Terence Tao.

Online Collaborative Projects

• The goal of such a project is to formalize a piece of mathematics. There are at least two aspects to this:
  1. Finding a way to represent mathematical objects in a programming language.
  2. Using the typing constraints of that programming language to check the syntactical correctness of a mathematical statement.
• Various formalization projects in Lean focus on the verification of mathematical proofs, in a variety of research fields:
  • The Liquid Tensor Experiment (condensed mathematics).
  • The Prime Number Theorem.
  • The sphere eversion theorem.
  • The generalized Carleson's theorem.

Collaboration tools

• A formalization project can involve tens of different people. Once the project is broken into subgoals, it is possible for people from distinct areas of research or with different levels of experience to work together.
• Discussion happens online, in the Lean Zulip channel, and the code repository is hosted on GitHub or a similar service.
• Recent efforts include developing the automation of certain tasks, sometimes using large language models (AI).

Blueprints

• A Lean blueprint establishes an interface between a mathematical text in the classical sense, written in , and its Lean code counterpart.
• It generates a dependency graph, showing the advancement of the formalization process (not formalized, statement formalized, proof formalized).
• The blueprint gets updated as the Lean code is being written.

The Blueprint for Fermat’s Last Theorem

Kevin Buzzard is currently leading the formalization of Fermat's Last Theorem (2024-2029). The big picture for the proof can be visualized as follows thanks to Lean blueprint:

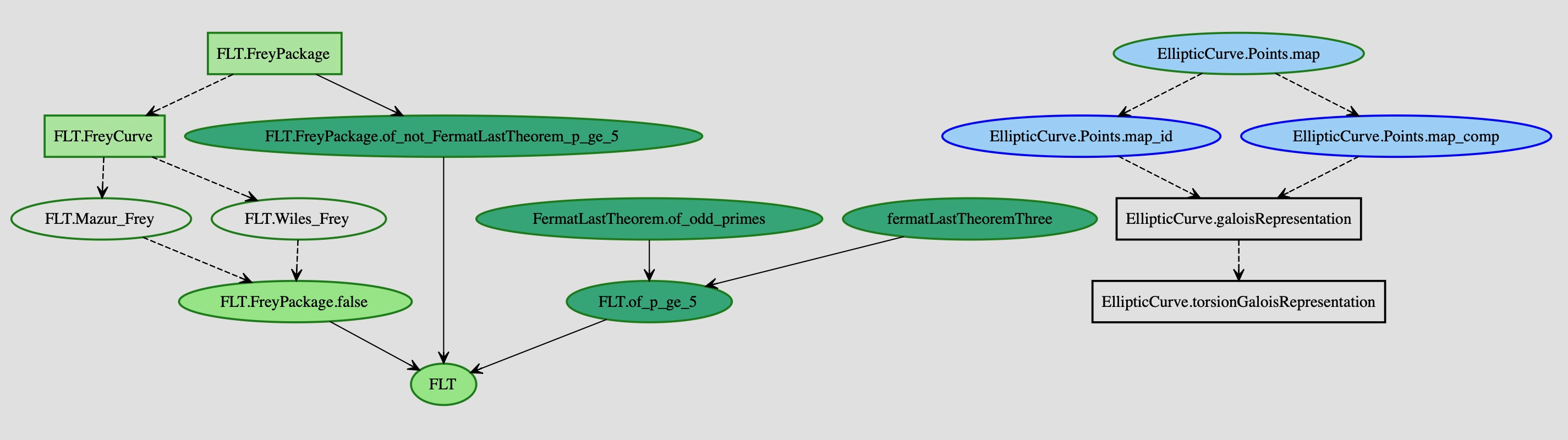
The colour code shows the advancement of the project towards completion.

Documentation

The following tools are indispensable when writing Lean code:

• The Mathlib documentation. It also includes Lean's core library and Batteries. The search is conducted by name (identifier).
• Loogle: the official Lean language search engine. There it is possible to search for a given type signature, such as (?a -> ?b) -> List ?a -> List ?b.
• Moogle and LeanSearch: AI-powered search engines. There you can use natural language, such as ​order subgroup divides order group or dim V = dim (Ker u) + dim (Im u).

Reference manuals

The following web-based books are the standard references of the Leanprover community:

• Theorem Proving in Lean 4, by Jeremy Avigad, Leonardo de Moura, Soonho Kong and Sebastian Ullrich (based on the 2017 Lean 3 version).
• Mathematics in Lean, by Jeremy Avigad and Patrick Massot (2020).
• Mechanics of proof, by Heather MacBeth (2022-2024).
• Functional Programming in Lean, by David Thrane Christensen (2023).

Lake and Reservoir

• Lean's build tool and package manager is called Lake (lean make).
• To start a Lean project, you can use lake init or lake new (try lake --help first). This can also be done directly from within VS Code, using the Lean 4 extension.
• Lean's packages can be hosted on Reservoir, Lean's package registry.

Basic Lean syntax

1. Terms and types
2. Curried functions
3. Inductive types

What is a type?

Depending on who you ask, a type may be seen as:

• An annotation to a term, controlling the operations that are permitted on that term: (3 : Nat), (-4 : ℤ), ([1, 2, 3] : List Nat), (Nat.mul : Nat → Nat → Nat).
• A list of rules to introduce and eliminate certain terms.
• A good substitute for the notion of topological space.

Every term has an assigned type, which is part of its definition as a term: since they do not have the same type, (3 : Nat) and (3 : ℤ) are different objects. Expressions such as x := x + 1 are not well-typed and do not make sense in a functional programming language.

Well-typed expressions

In Lean, you can find out the type of a term by using the #check command:

#check 42             -- 42 : Nat
#check Nat            -- Nat : Type
#check Nat.mul        -- Nat.mul : Nat → Nat → Nat
#check "42"           -- "42" : String
#check 1 + 1          -- 1 + 1 : Nat
#check 1 + 1 = 2      -- 1 + 1 = 2 : Prop
#check 1 + 1 > 2      -- 1 + 1 > 2 : Prop

Note that a well-typed expression can be recognised as a proposition regardless of whether it is "mathematically correct". The expression 2 + 2 = 5, for instance, is syntactically correct (an equality between two natural numbers). In contrast, a common expression such as 2 * (3 + 1) = 2 * 3 + 2 * 1 = 8 is not well-typed.

Why bother?

It is common sense not to mix quantities that are not related to one another. Here is an example of an ill-typed expression.

Image credits: MikeGogulski, CC BY-SA 3.0.

The development of type theory

• Types were introduced by Bertrand Russell in 1912, with the hope of avoiding the emergence of paradoxes in set theory.
• Their usage was systematised and simplified by Alonzo Church, who introduced the (simply-typed) -calculus in 1940.
• In 1972, Per Martin-Löf developed a dependent type theory that can be used as an alternative foundation of mathematics. This is the underlying logic of Lean.
• In 1989, Thierry Coquand released the first official version of Coq (a.k.a. Rocq), a proof assistant that supports all the constructs of Martin-Löf type theory.
• In 2013, Vladimir Voevodsky and his collaborators published a treatise on Homotopy Type Theory, which is the basis for the univalent foundations of mathematics.

Structure of a proof assistant

The architecture of an Interactive Theorem Prover can be represented as follows.

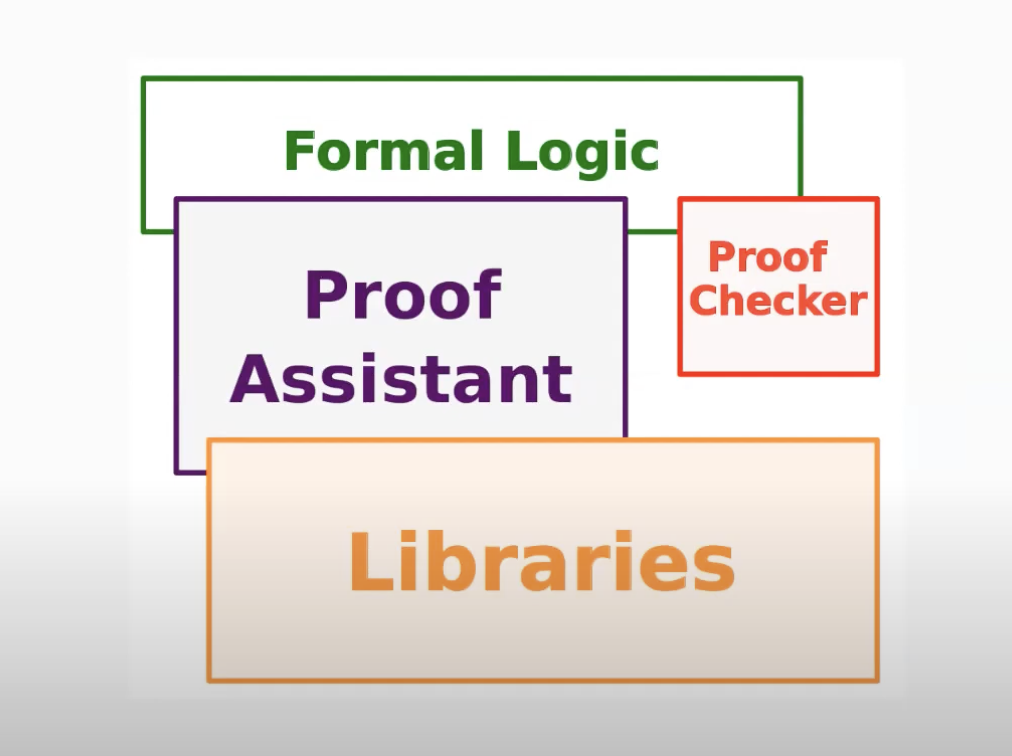Image credits: Assia Mahboubi.

• Human users interact with the proof assistant by writing libraries.
• The compiler checks that the code is syntactically correct.
• The choice of type theory as the underlying logic is a design choice.

Mathematical functions

• Simply-typed functions f : X → Y are the basic objects of a language like Lean.
• Their implementation can look similar to the usual mathematical definition:

def fact : Nat → Nat
  | 0     =>  1 
  | k + 1 => (k + 1) * fact k

#check fact    -- fact : Nat → Nat

#check fact 5  -- fact 5 : Nat

#eval  fact 5  -- 120

Curried functions

• The natural way to define a function of two variables in Lean is to use curried notation.
• A function of two variables can be replaced by a function that sends to a function of , namely .
• In functional programming languages, when we write f : A → B → C, then, in the expression f a b, the term f a is a function from B to C, and it is applied to b.

def sum : Nat → Nat → Nat := fun x y ↦ x + y

#check sum 3    -- sum 3 : Nat → Nat
#eval  sum 3 5  -- 8

If we set instead def sum₁ : Nat → Nat → Nat := fun x ↦ (fun y ↦ x + y), then we get sum = sum₁, by reflexivity.

Higher-order functions

• We can write curried functions with an arbitrary number of variables: if f : A → B → C → D → E, then for all a : A, b : B, c : C, d : D, we have f a b c d : E.
• This is not the same as f : A → (B → C) → D → E, which takes as arguments a term a : A, a function u : B → C and a term d : D, returning a term of type E.

def f : Nat → (Nat → ℝ) → ℝ → ℝ := 
  fun (n : Nat) (u : Nat → ℝ) (x : ℝ) ↦ 2 ^ n * u n + x

def v : Nat → ℝ := fun n ↦ 2 * n

#eval f 3 v (-6)  -- 42

Inductive types

The most famous inductive type in mathematics is probably the type Nat, whose definition goes back to Giuseppe Peano in 1889.

inductive Nat : Type
  | zero : Nat
  | succ : Nat → Nat

Inductive definitions produce special functions called constructors. In the present case, there are two of them (two introduction rules for terms of type Nat):

• Nat.zero : Nat (a function whose value is its own name is called an atom, you can view it as a function from the Unit type to Nat, if you prefer).
• Nat.succ : Nat → Nat (the successor function), saying that for every n : Nat there is a term n.succ : Nat (dot notation for Nat.succ (n : Nat)).

Product types are inductive types

The fact that product types are defined inductively may seem less familiar to mathematicians.

inductive Prod (X Y : Type) : Type
  | mk : X → Y → Prod X Y

This means that terms of type Prod X Y are introduced via the constructor Prod.mk : X → Y → Prod X Y. In other words, for all x : X and all y : Y, the term Prod.mk x y is of type Prod X Y and this is the only introduction rule for terms of type X × Y. In Lean, the type Prod X Y is denoted by X × Y and its terms by ⟨x, y⟩ (angle brackets).

Functions defined on inductive types

• We have already seen examples of a functions f : Nat → Nat, namely the factorial function. It was defined by induction. Since the constructor Nat.succ is a function from Nat to Nat, the induction principle for Nat includes a recursive call: to define f (n + 1), we may use n and f n, as in the definition of fact (n + 1).
• However, induction is not limited to Nat: every inductive type has an associated induction principle. For the product, it implies in particular that, in order to define a function f : X × Y → Z, it suffices to define it on the canonical terms Prod.mk x y. In practice, this is done via pattern matching.

def proj₁ {X Y : Type} : X × Y → X
  | Prod.mk x y => x

The sum of two types

• The sum of two types and is also defined inductively.
• The inductive type has two constructors because there are two ways to introduce terms of type : they come either from or from .
• To eliminate terms of type into , we have to specify the definition of our function on each constructor. This is done by pattern matching (case analysis).

inductive Sum (X Y : Type) : Type
  | inl : X → Sum X Y
  | inr : Y → Sum X Y

def charac_second_summand {X Y : Type} : X ⊕ Y → Bool
  | Sum.inl x => (false : Bool)
  | Sum.inr y => (true  : Bool)

Wrap-up and where to go from here

• Functional programming languages based on dependent type theory with inductive types (such as Lean 4) can be used to formalise mathematics.
• Type-checking means verifying that our code is syntactically correct.
• Curried functions and inductive types are used in a variety of contexts and for many purposes, in particular to formalise mathematics.
• To each inductive type there is associated an induction principle. It enables us to define functions out of an inductive type by pattern matching.
• Now let us write some Lean code !

Practice file on Lean syntax and link to the Natural Number Game

Lean syntax Natural Number Game

Piece of trivia: often seen in Lean examples, is the lowest irregular prime. An odd prime number is irregular if there exists a natural number such that divides the numerator of the -th Bernoulli number (Kummer's criterion).