Algebra, Logic, and Proof Visualization

Florent Schaffhauser, Heidelberg University.
Illustrating Mathematics: Reunion / Expansion. ICERM, 11-15 August 2025.

The gist

• A quick report on a student seminar held in Heidelberg in the Fall of 2024.
• Students investigated the use of an Interactive Theorem Prover to create an online game to study basic notions of number theory (prime versus irreducible elements).
• The report will be published in the Communications of the German Mathematical Society.
• The goal was to find ways to represent mathematical objects and proofs using a programming language and experiment with them.

structure IsPrime {R : Ring} (p : R) : Prop where
  not_unit : IsUnit p → False
  div_prod : ∀ a b : R, p | a * b → p | a ∨ p | b

The Lean game server

• Hosted by the Heinrich Heine Universität in Düsseldorf. Offers various games already (and the possibility to host yours).
• The most famous Lean game among mathematicians is probably the Natural Number Game, created for Lean 3 by Kevin Buzzard and Mohammad Pedramfar, to serve as an introduction to Lean tactics. Be sure to try it out and see if you get hooked!
  
• Recently, a game about Discrete Mathematics in Lean was added. There is also one about Knights and knaves, which formalizes a famous puzzle in Lean.

Illustrating Mathematics: Reunion / Expansion

• Mid-career mathematician working in the field of complex geometry.
• Research interests: Higgs bundles, Fuchsian groups.
• Recently moved from Bogotá (2010-2022) to Heidelberg (since 2022).
  
• Activity since 2023:
  • Developing an interest in formal mathematics and homotopy type theory.
  • Managing Director of the Heidelberg Experimental Geometry Lab (HEGL).

Undergraduate seminars and student activities

• Through HEGL:
  • Illustrating Mathematics seminar.
  • Teaching Mathematics seminar.
    
• Outside HEGL:
  • Computer-assisted Mathematics seminar (Sage + Lean).

The 2024 HEGL Illustrating Mathematics seminar

• Was about Algebra, Logic, and Proof Visualization.
• Claim: formal mathematics is a way to represent mathematical objects, in particular proofs.
• Challenge: Make this a dynamical process by using a proof assistant to create an online game, learn some new math in the process.
  

The Lean programming language

• Is a (relatively new) programming language that can be used to formalize mathematics (Lean 4 was released in 2021, the initial version of Lean was 2013).
• Lean benefits from a modern infrastructure, currently under rapid development.
• Other comparable options are: Rocq, Agda.

def fact : Nat → Nat
| 0     =>  1 
| k + 1 => (k + 1) * fact k

#eval  fact 5  
  -- 120

theorem fact_succ (n : Nat) : fact (n + 1) = (n + 1) * fact n := 
  rfl

Formalizing mathematics

• Often reduced to checking correctness but is first and foremost about giving a representation of mathematical objects.
• Requires some brain rewiring, namely learning a bit of type theory, hence also some logic.

• The latter requirement is easily accepted by students but can generate some pushback from colleagues (even before getting to the computer-assisted part).

Type theory

• Has been developing for more than a century: Russell (1905), Church (1941), Martin-Löf (1973), Voevodsky and collaborators (2013).
  
• Emerges from logic, in particular the rules of natural deduction (Gentzen).
• Can serve as a foundation both for mathematics and for programming languages.
• The Lean system is incompatible with Voevodsky's univalent mathematics.

Propositions-as-types / Proofs-as-programs

• Often referred to as the Curry-Howard correspondence.
  
• Fundamental aspects:
  • Mathematical concepts are represented as types (and proofs as terms).
  • The logic is not postulated oustide the theory: it is intuitionnistic (introduced in the language itself) and constructive (no axioms).
• In Voevodsky's approach, types are viewed as spaces / homotopy types.

An example

• An implication is represented by the type of functions from . The modus ponens rule is then just evaluation of functions.

• In general, we only have , as the converse requires a proof of . Below is a proof of the direct implication, using pattern matching.

example {P Q : Prop} : (¬P ∨ Q) → (P → Q)
| Or.inl (notP : ¬P) => fun (p : P) ↦ False.elim (notP p)
| Or.inr (q : Q)     => fun (_  : P) ↦ q

• Here, is a type used to denote absurdity and negation is defined as .

Mathematical structures

• Martin-Löf's type theory is often referred to as dependent type theory (as opposed to Church's type theory, which is sometimes referred to as simple type theory).
• Properties such as the commutativity of a ring can be represented quite naturally using dependent types.
• In this approach, a commutative ring is a pair (R, mul_comm) where R is a ring and mul_comm is a proof that the multiplication operation of R is commutative.

structure CommRing where
  R        : Ring
  mul_comm : ∀ x y : R, x * y = y * x 

• Note how the type representing the commutativity property depends on the term R introduced one line above. A ring is itslef a a tuple .

A visualization challenge

• In the 2024 HEGL seminar, the first half of the semester was dedicated to learning the concepts we have just discussed, and what it implies for basic concepts of algebra.
  

• The students were then asked to write a Lean proof that, in a domain, every prime element is irreducible, and to turn that proof into a game.

The pen-and-paper proof

• Mines, Richman and Ruitenburg tell us that the natural setting for the proof of prime irreducible is that of cancellative commutative monoids. We can just think of the positive natural numbers .
• Assume that is prime and that . We want to show that is invertible or is invertible.
• Since , we have . As is prime, this implies that or .
  • If , then we can find such that . So , which implies that , i.e. is invertible.
  • Similarly, if , then is invertible.
• As we shall see, the Lean proof is much longer! We can see it in Lean4Web, where we can also modify it.

Paperproof

• Paperproof is a VS Code extension that gives a visual representation of a Lean proof.
• The highlighting changes as one scrolls down the proof.
  

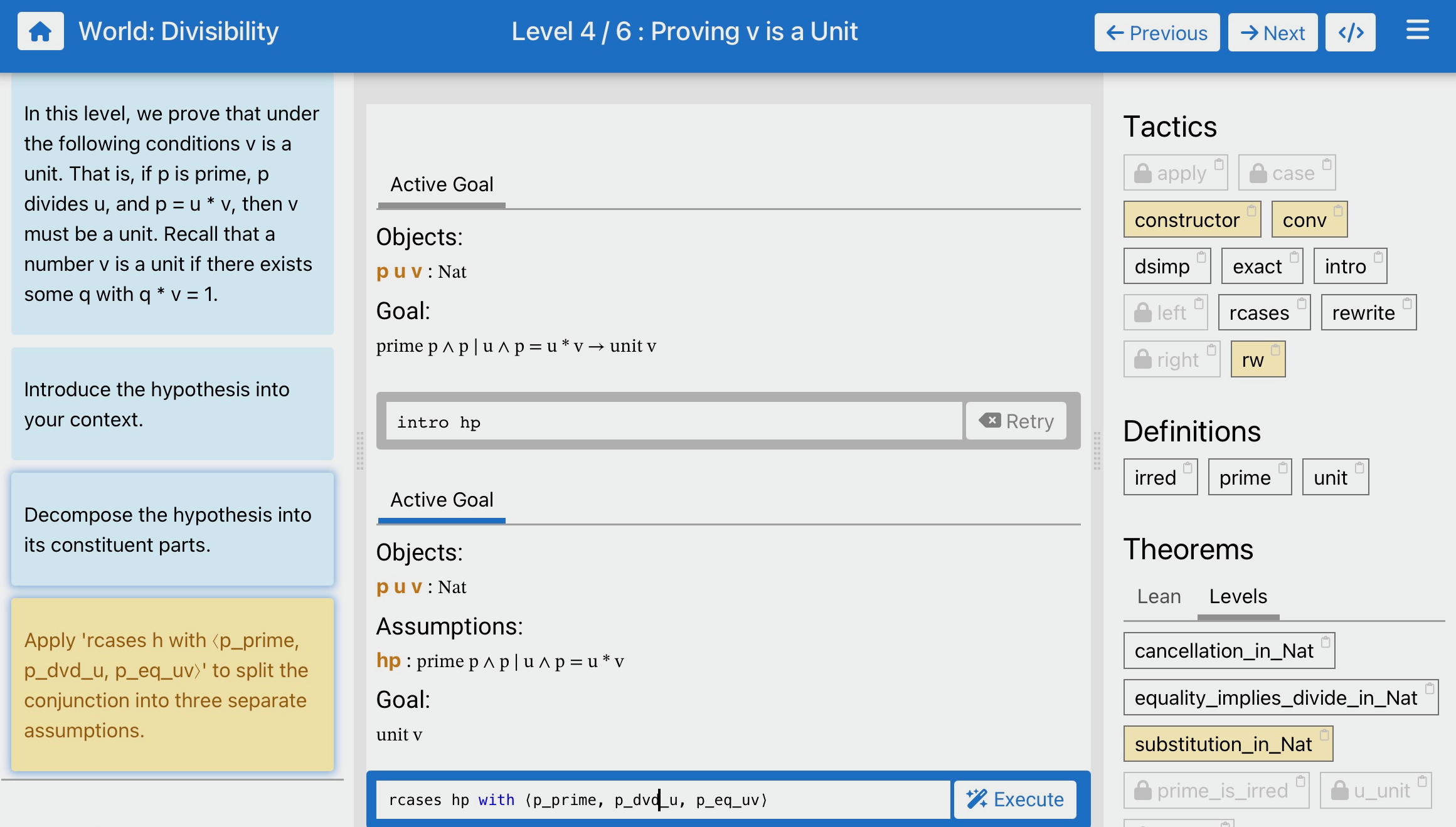
The game interface

• A game consists of several worlds, and each world of several levels. We created our levels by splitting the proof that irreducible prime into various steps.
• Thanks to the interface, we can provide hints and explanations via clickable links.
  

Feedback / Next steps

On the up side:

• The students were engaged and participating actively the whole semester (not just for their own talk).
• Writing a game is a good way to get acquainted with the use of a proof assistant.

On the down side:

• Lean's syntax is difficult to grasp at the beginning and this can hinder the learning experience. Teaching completely new concepts directly with Lean does not work well.
• The game interface is still very close to the syntax and this is not quite game-like, even though it is a good way to learn to use Lean.

To keep exploring this seems like a fun activity for future iterations of the seminar!