Logic, proof and visualization

HEGL Illustrating Mathematics Seminar
Winter Semester 2024-2025

Florent Schaffhauser
Heidelberg University

Sets and logic

• Today's lecture is about language.

• To be able to discuss mathematical concepts, we need to give rules for:

  1. How to construct/introduce elements of a set.
  2. How to identify or distinguish those elements.

Example: the natural numbers

• Peano's natural numbers are defined inductively. Here is the definition in the Lean 4 programming language.

inductive Nat : Type
  | zero           : Nat
  | succ (n : Nat) : Nat

• There is a natural number called zero and a function succ : Nat -> Nat called successor that, from a given natural number n, constructs a natural number succ n.
• So, using zero and succ we can construct succ zero, then succ (succ zero), etc.

Notation

• We denote the natural numbers by . We write:
  • 0 instead of zero,
  • 1 instead of succ zero,
  • 2 instead of succ (succ zero),
  • etc.
• Is 0 ≠ 1 and what does that mean?
• Does succ n = succ m imply n = m?

Equality

• Equality is a relation between elements of a set.
• Inequality can be defined as the negation of equality.
• Can we supply formal definitions for these concepts?

For instance, we want succ n = n + 1 for natural numbers. How do we define + and check that the former equality holds?

Equivalence relations

We expect the equality relation on a set to be:

• Reflexive, meaning that, .
• Symmetric, meaning that, .
• Transitive, meaning that, .

A binary relation satisfying these properties is called an equivalence relation.

Propositions

Given a set , expressions such as , or , or are examples of propositions.

This does not mean that they represent true statements!

It also does not mean that we can somehow evaluate their "truth value" by applying a "know-it-all" function.

The question is whether we can construct a proof of these propositions.

Propositions as sets

• Propositions, just like sets, may or may not have elements (usually called proofs).
• When we look at an equality between two elements in a set, we ask ourselves: can we construct a proof of ? This is usually a hard question!
• To answer it, we must provide a formal definition of equality.

Implications and conjunctions

• Let and be propositions. What does mean? And what does mean?
• In our language, these are defined constructively, just like sets.
• And just like for sets, we must provide rules to construct/introduce proofs.

Implications

Let and be propositions.

• We want to be a proposition, so we ask ourselves: what does it mean to construct a proof of ?
• From the analogy with sets, it means constructing a function from to .
• So, to prove , we must write a program that takes a proof of as input and returns a proof of as output.

Conjunctions

Let and be propositions.

• What does it mean to prove the conjunction ?
• It is the proposition whose proofs consists are constructed from pairs where is a proof of and is a proof of .

inductive And (P Q : Prop) : Prop
  | intro (p : P) (q : Q) : And P Q

Example: successor of an even number

Let be a natural number.

• Let and let . Then we should be able to construct a proof of the implication .
• Indeed, given a and a proof that , we should be able to deduce that , using that same .
• This suggests that a proof of should be constructed from a dependent pair where and is a proof that .

Big idea (# 1)

Propositions behave similarly as sets.

• To specify a proposition, we say how its proofs are constructed/introduced.
• We constructions new propositions from old ones using functions, products, and other such rules.
• This is known as the Curry-Howard correspondence or the Brouwer-Heyting-Kolmogorov interpretation.

Negation

Just like for sets, there is an empty proposition called or ⊥ (bottom). It is defined by the absence of way to construct proofs of it.

inductive False : Prop

• The negation of a proposition is defined as the proposition , usually denoted .
• To prove , we must construct a function from to , meaning show that, from a proof of , we can derive a proof of .
• Can you see why, given a proposition , we have ?

Denial inequality

• If we have an equality relation , we can always define the denial inequality (the negation of equality).

• Do we have in natural numbers and how do we prove this?

Possible project: the natural numbers

1. Injectivity of Nat.succ and proof that, ∀ n : ℕ, 0 ≠ succ n.
2. Definition and properties of addition and multiplication of natural numbers.

Proofs of equality

• It is difficult to define equality, i.e. to give rules for how to prove an equality.
• In 1973, Martin-Löf proposed to define equality inductively, with reflexivity as the only way to construct a proof:
  Symmetry and transitivity of equality then follow from reflexivity, by induction.
• In Martin-Löf's approach, equality is no longer observed, it is carried. Frege conceptualizes this difference using the words Bedeutung and Sinn (1892).

Congruence and transport (substitution)

• The following properties of equality are also proved by induction.
• If is a function and in , then .
• Given a family of propositions depending on a parameter , if in , then .

Martin-Löf's constructive mathematics

• A constructive proof is a algorithmic in nature. It can, in principle, be converted into a computer program.
• The fact that the program typechecks is a proof that the algorihtm is correct, meaning that it meets its specification.
• This is the reason why type theory is the theoretical foundation of modern functional programming languages, and why these can be used as proof assistants.

Structure of an interactive theorem prover

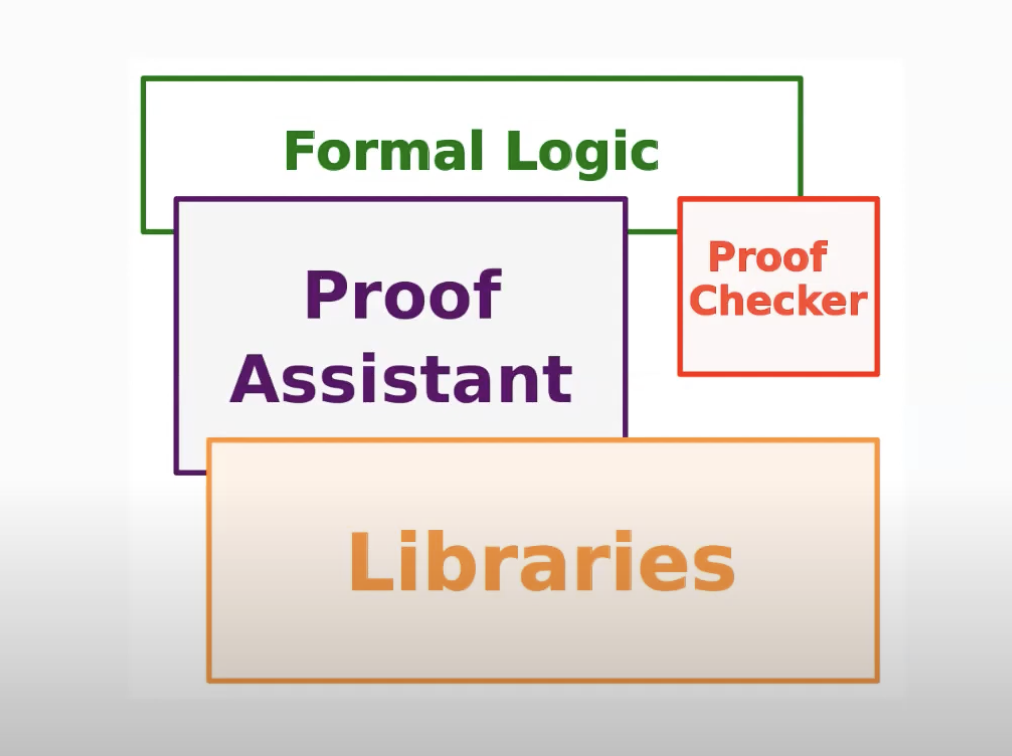
Image credits: Assia Mahboubi.

Disjunction

Let and be propositions.

• What does it mean to construct a proof of ?
• By definition, it means providing either a proof of or a proof of .

inductive Or (P Q : Prop) : Prop
  | inl (p : P) : Or P Q
  | inr (q : Q) : Or P Q

• This means that there are two ways of constructing a proof of .

Tautologies

A tautology is a proposition which is built up from older ones and which has a proof regardless of whether the old ones do. For instance:

• , , .
• , , .
• , .
• .
• .
• , , .

Possible project: Propositional calculus

1. Prove the previous tautologies.
2. Prove De Morgan's first law: .
3. Prove the implication: .

Here, is defined as

Existential statements

• What does it mean to prove that ?
• By definition, it means to provide a pair where is and is a proof of the equality . In Lean, the proposition is defined as follows.

inductive Exists (P : X → Prop) : Prop
  | intro (x : X) (p : P x) : Exists P

• So, formally, proofs of an existential statement are dependent pairs: they are terms of the form , where and .

Constructive proofs of existence

• Let be the proposition such that and are irrational and is rational and consider the following proof for it. If is rational, then we can take . Otherwise, we can take and .
• This is classical reasoning: we are assuming that we can prove , where is the proposition that is rational. Constructively, we have only proven that

Universal statements

Proofs of universal statements are somewhat trickier.

• Let for instance be the proposition is even. We can think of as a family of propositions depending on the parameter . For a fixed , the proposition says that is even, and we know how to construct a proof of this.
• But what does it mean to provide a proof of ? To do that, we need the concept of a dependent function, for which the target space depends on the input value.

• For , the term is an element of , meaning that is a proof of the proposition .

Big idea (# 2)

Mathematical logic is not a pre-requisite of our language. Instead, logical connectives and quantifiers are introduced in the same way as sets.

Decidability

• We will be particularly interested in sets with decidable equality, i.e. sets for which the following proposition has a proof:
  where is the denial inequality.
• More generally, a proposition is called decidable if the proposition has a proof.
• Sets with decidable equality are sometimes called discrete sets. If we accept the LEM, then all sets are discrete ().

Possible project: Sets and subsets

• Show that the set of natural numbers has decidable equality.
• Given a set , a predicate defines a subset . Show that if has decidable equality, then has decidable equality.
• Let be the subset of defined by the predicate . What predicates define and ? Show that .
• Show that if, for all , is decidable, then .

Uses of decidability

The equivalences in can be taken as definitions of and in classical logic, where by the law of excluded middle (LEM), every proposition is decidable.

• If is decidable, then .
• If is decidable, then .
• If is decidable, then .
• If and are decidable, then
• If and are decidable, then we have De Morgan's second law: .

In , we have the tools of classical reasoning. In , we have the double negation, which holds if the LEM holds.

Possible project: Predicate calculus

Let be a predicate on a set .

1. Prove the equivalence .
2. Find decidability conditions under which we can prove the equivalence .
3. How about ? And ?

As an example, think of the statement that, given an ideal in a ring , there exists in and in such that . How do we prove this in the ring , say?